Homogeneous coordinates 齐次坐标

#发芽

[!维基百科] 在 数学 里，齐次坐标（homogeneous coordinates），或投影坐标（projective coordinates）是指一个用于 投影几何 里的坐标系统，如同用于 欧氏几何 里的 笛卡尔坐标 一般。

• 是一种扩展的坐标系统，将原来 $n$ 维的向量用一个 $n+1$ 维的向量来表示，新增的维度可视作原向量的缩放系数
• 是在 [[ 透视空间 ]] 中对点的描述

缘由

• 为了处理 [[ 透视空间 ]] 中的问题，两条平行线可以相交于一点
• 通过引入额外的维度使得 坐标变换 能够用矩阵乘法的形式进行简洁而统一的表示

说明

^ee6ccd

• 给定欧氏平面上的一点 $(x, y)$，$x, y$ 不全为零，对任意非零实数 $Z$，三元组 $(xZ, yZ, Z)$ 即称之为该点的齐次坐标。
• 齐次坐标可将无穷远处的点以有限坐标的形式进行表示，即 $(x, y, 0)$ 表示一无穷远点。
• 一个点可以有无限多个齐次坐标表示法。
• 对二维点 $P(x, y)$ 的齐次坐标 $(xZ, yZ, Z)$，可以理解为在三维坐标系中，原点 $(0, 0, 0)$ 与点 $(x, y, 1)$ 射线上的任意一点均表示该点 $P$。即在 [[ 透视空间 ]] 中，相交于一点的平行线

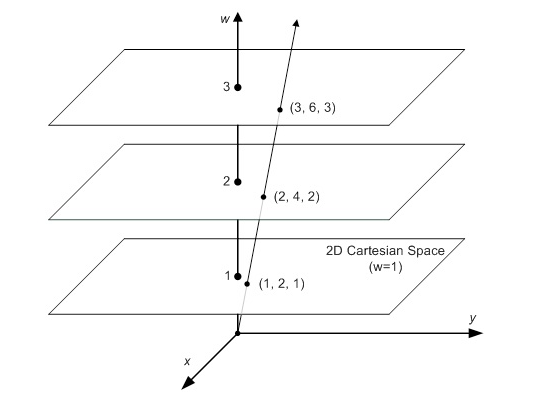
实例

• 二维空间的齐次坐标

类比

[!note] 记录与该概念类似的概念，属于 how 的部分

对比

• Cartesian Coordinates 笛卡尔坐标

效果

[!note] 记录该概念如何解决实际问题，属于 how good 的部分

备注

• 维基百科 - 齐次坐标