Transformation 变换

最后修改于 2023-07-18

阅读量:[object Object]

模型变换（Modeling）和视图变换（Viewing）

WHY

描述移动、旋转、缩放和投影操作对图像的影响

视图变换 Modeling

缩放变换 Scale

缩放矩阵 Scale Matrix

[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} s_{x} & 0 \\ 0 & s_{y} \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]

当进行均匀缩放时， $s_{x} = s_{y}$ ；不均匀缩放时， $s_{x} \neq s_{y}$ 。

缩放矩阵符号表示： $S S_{s_{x}, s_{y}}$ ，其中 $s_{x}, s_{y}$ 分别表示在 $x$ 方向和 $y$ 方向上的缩放系数。

反转矩阵 Reflection Matrix

[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]

切变 Shear Matrix

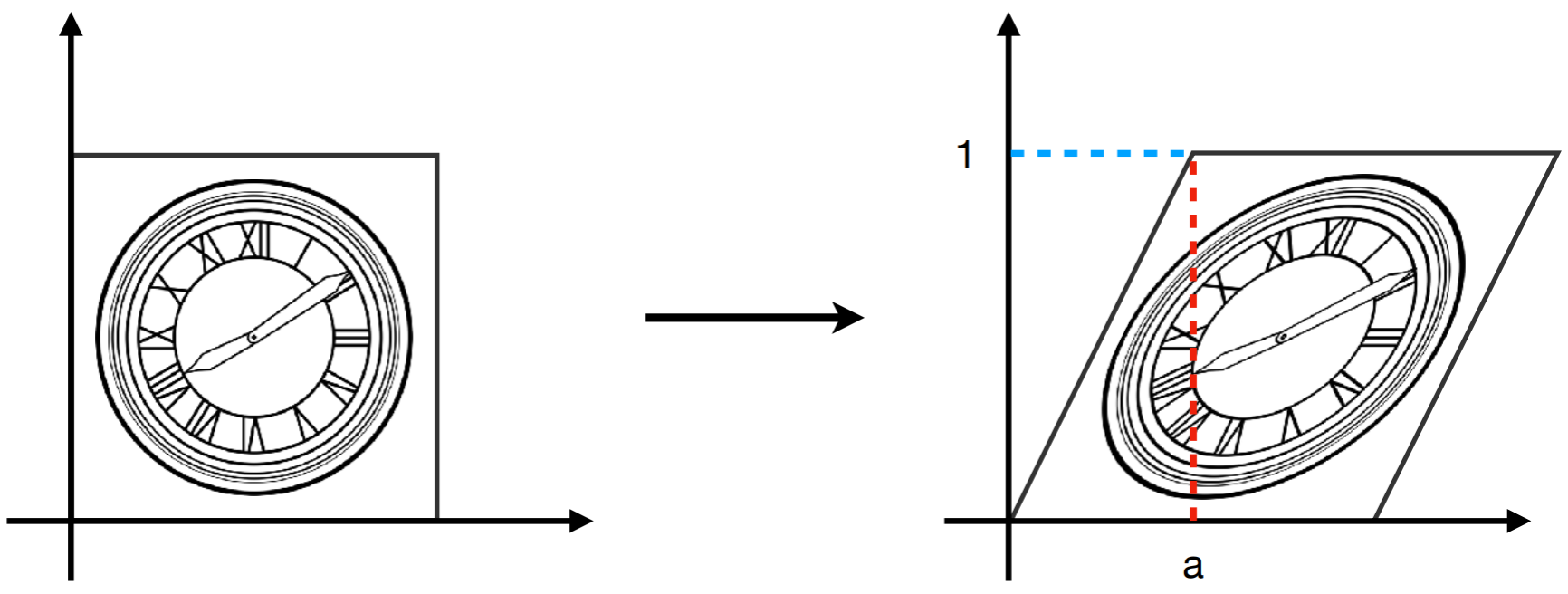
Transformation 变换 figure 1.png

[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 1 & a \\ 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]

根据变换前后的对应函数关系确定变换矩阵。

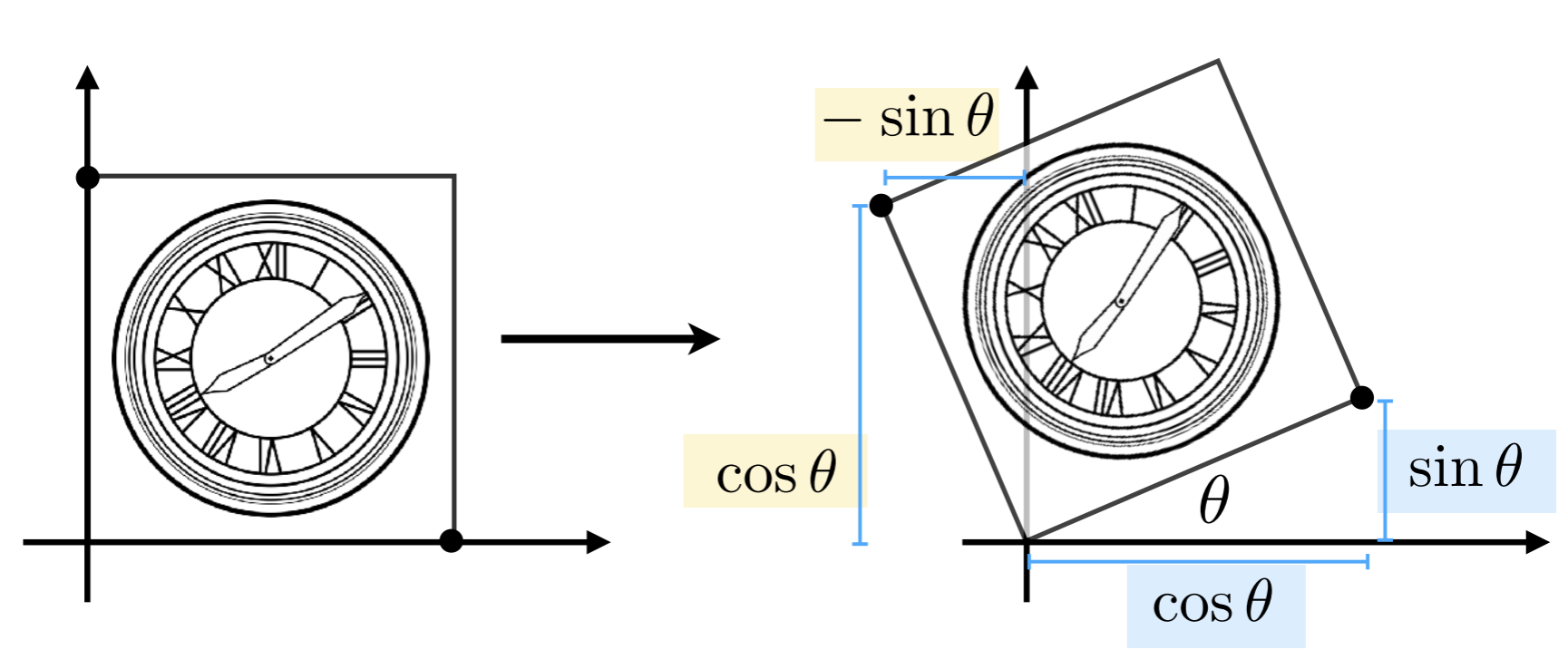
旋转变换 Rotate

^04bbec

默认绕原点，逆时针方向进行旋转。

旋转矩阵 Rotation Matrix

Transformation 变换 figure 2.png

R R_{θ} = [\begin{matrix} c o s θ & - s i n θ \\ s i n θ & c o s θ \end{matrix}]

平移变换 Translation

^9c5863

x^{'} = x + t x

y^{'} = y + t y

平移变换无法仅使用矩阵乘积的形式进行描述，因此引入齐次坐标，将所有的变换均可仅用矩阵乘积的形式进行描述。

平移变换的矩阵形式（齐次坐标）

[\begin{matrix} x^{'} \\ y^{'} \\ w^{'} \end{matrix}] = [\begin{matrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}] = [\begin{matrix} x + t_{x} \\ y + t_{y} \\ 1 \end{matrix}]

仿射变换 Affine Transformation

仿射变换 = 线性变换 + 平移变换

缩放、旋转均为线性变换

先线性变换，再平移变换

[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} a & b \\ c & d \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] + [\begin{matrix} t_{x} \\ t_{y} \end{matrix}]

在齐次坐标中

[\begin{matrix} x^{'} \\ y^{'} \\ 1 \end{matrix}] = [\begin{matrix} a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}]

在表示二维仿射变换下，变换矩阵的最后一行为 $(\begin{matrix} 0 & 0 & 1 \end{matrix})$ 。

齐次坐标下的变换矩阵

缩放 $S S_{(s_{x}, s_{y})} = [\begin{matrix} s_{x} & 0 & 0 0 & s_{y} & 0 0 & 0 & 1 \end{matrix}]$
旋转 $R R_{α} = [\begin{matrix} c o s θ & - s i n θ & 0 s i n θ & c o s θ & 0 0 & 0 & 1 \end{matrix}]$
平移 $T T_{(t_{x}, t_{y})} = [\begin{matrix} 1 & 0 & t_{x} 0 & 1 & t_{y} 0 & 0 & 1 \end{matrix}]$

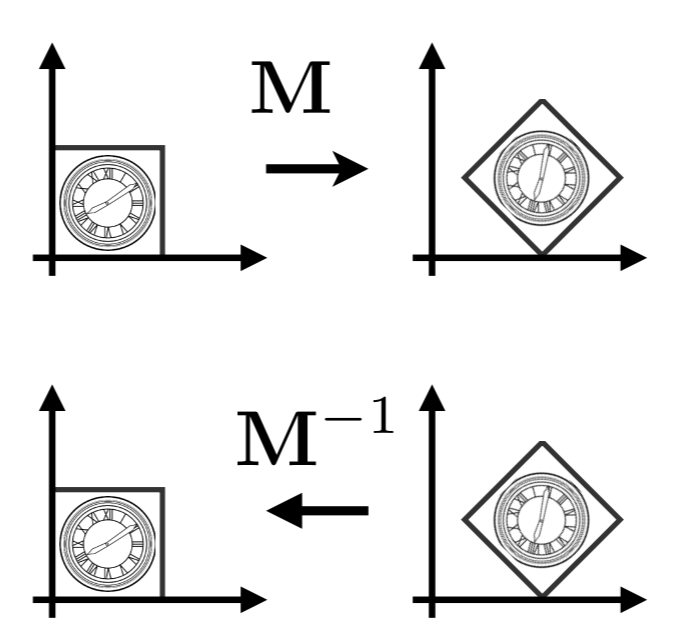
逆变换 Inverse Transformation

变换矩阵的逆矩阵 $M M^{- 1}$

Transformation 变换 figure 3.png

组合变换 Composing Transform

连续进行多种不同的变换。变换的顺序对变换结果有影响，即

R R_{45} \cdot T T_{(1, 0)} \neq T T_{(1, 0)} \cdot R R_{45}

变换矩阵按照变换顺序从右向左相乘，例如，先旋转 $45^{\circ}$ ，再平移 $(1, 0)$ ：

T T_{(1, 0)} \cdot R R_{45} \cdot [\begin{matrix} x \\ y \\ 1 \end{matrix}]

一系列仿射变换： $A A_{1}, A A_{2}, \dots, A A_{n}$

A A_{n} (\dots A A_{2} (A A_{1} (x))) = A A_{n} \cdot \dots \cdot A A_{2} \cdot A A_{1} \cdot [\begin{matrix} x \\ y \\ 1 \end{matrix}]

可先计算所有的变换矩阵，得到一个变换矩阵，提高效率。

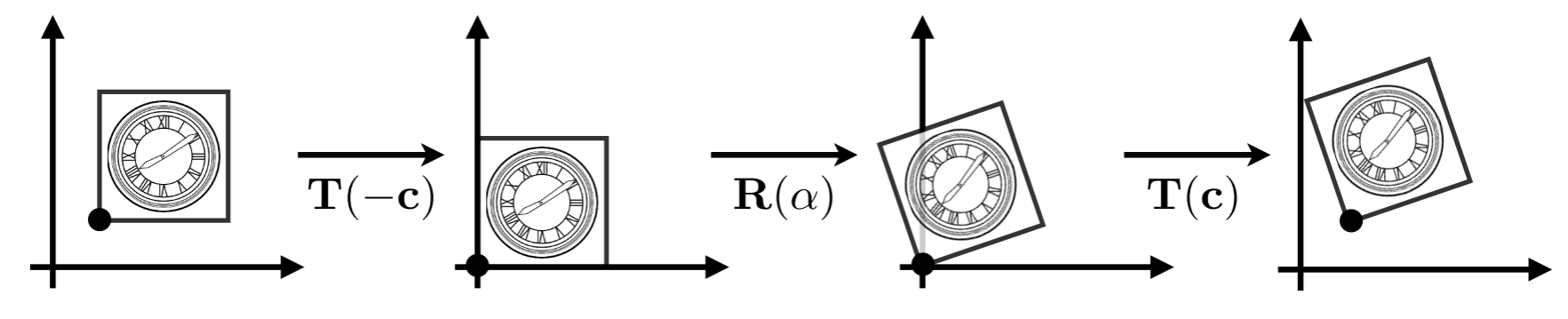
复杂变换分解 Decomposing Complex Transformation

以任意点 $c$ 为中心进行旋转，可结合平移和旋转将复杂变换转化为几种简单变换的组合。

将点 $c$ 平移至中心
旋转
平移至原来的状态

T (c) T (c) \cdot R (α) R (α) \cdot T (- c) T (- c)

在三维变换中，沿任意轴进行旋转可采用同样的思路。

三维变换 3D Transformation

三维空间下的齐次坐标：

点 $(x, y, z, 1)^{T}$

向量 $(x, y, z, 0)^{T}$

三维仿射变换可用 $4 \times 4$ 的矩阵进行表示

[\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \\ 1 \end{matrix}] = [\begin{matrix} a & b & c & t_{x} \\ d & e & f & t_{y} \\ g & h & i & t_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}]

#待整理笔记

反向链接

坐标变换

#播种

Av 二维向量坐标系变换实例（齐次坐标）

#开花

Computer graphics 计算机图形学

基础知识：

到头儿啦~