Probability distribution 概率分布

概率分布（Probability Distribution）或简称分布，是 概率论 的一个概念。使用时可以有以下两种含义：

• 广义地，它指称随机变量的概率性质 – 当我们说概率空间 $(\Omega ,{\mathcal {F}},\mathbb{P})$ 中的两个 随机变量 $X$ 和 $Y$ 具有同样的分布时，我们是无法用概率 $\mathbb{P}$ 来区别他们的。换言之：

称 $X$ 和 $Y$ 为同分布的随机变量，当且仅当对任意事件 $A \in \mathcal{F}$，有 $\mathbb{P} (X \in A)= \mathbb{P} (Y \in A)$ 成立。

但是，不能认为同分布的随机变量是相同的随机变量。事实上即使 $X$ 与 $Y$ 同分布，也可以没有任何点 $\omega$ 使得 $X(\omega)=Y(\omega)$。在这个意义下，可以把随机变量分类，每一类称作一个分布，其中的所有随机变量都同分布。用更简要的语言来说，同分布是一种等价关系，每一个等价类就是一个分布。需注意的是，通常谈到的离散分布、均匀分布、伯努利分布、正态分布、泊松分布等，都是指各种类型的分布，而不能视作一个分布。

• 狭义地，它是指随机变量的概率分布函数。设 $X$ 是样本空间 $(\Omega,\mathcal{F})$ 上的随机变量，$\mathbb{P}$ 为概率测度，则称如下定义的函数是 $X$ 的分布函数（Distribution Function），或称累积分布函数（Cumulative Distribution Function，简称 CDF）：

$F_{X}(a)=\mathbb {P} (X \leq a)$，对任意实数 $a$ 定义。

具有相同分布函数的随机变量一定是同分布的，因此可以用分布函数来描述一个分布，但更常用的描述手段是 概率密度函数（Probability Density Function, 简称 PDF）。

• 在常用的文献中，“分布”一词可指其广义和狭义，而“累计分布函数”或“分布函数”一词只能指称后者。

概率分布给出了所有取值及其对应的概率（少一个也不行），只对离散型变量有意义。例如：

针对连续型变量时，称作概率分布函数。

概率分布函数 $F(x)$：给出取值小于某个值的概率，是概率的累加形式，即：

$F(x_i)=P(x<x_i)=sum(P(x_1),P(x_2),…,P(x_i))$（对于离散型变量）或求积分（对于连续型变量）。

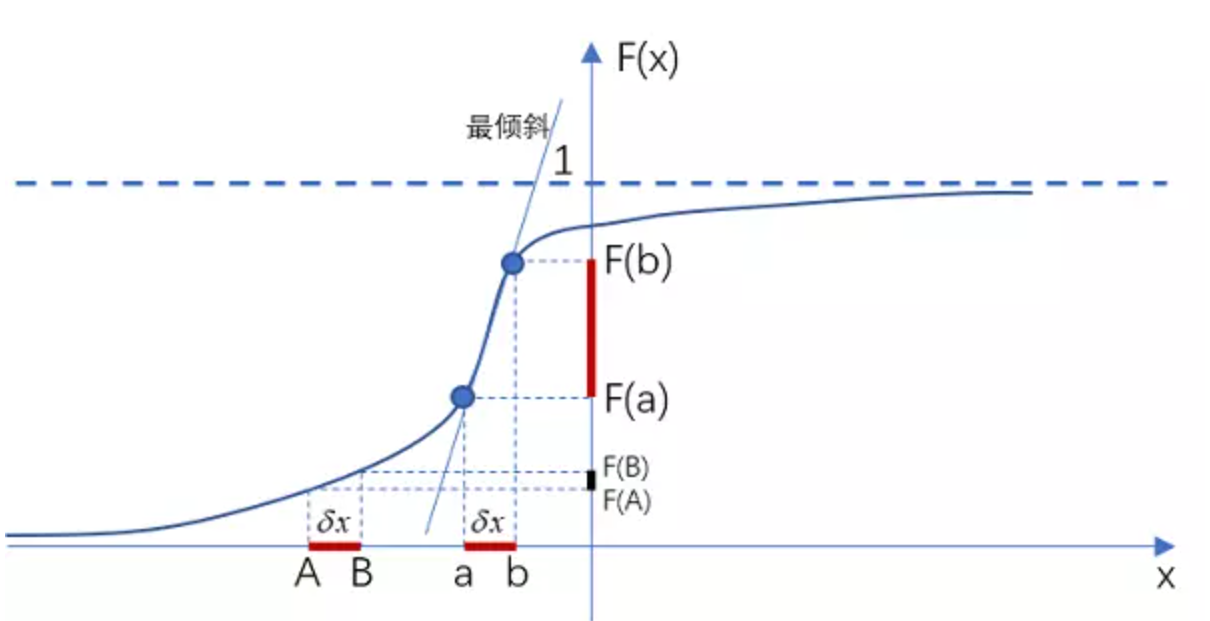
概率分布函数 F(x) 的性质：

1. $\forall a<b$，总有 $F(a) \le F(b)$（单调非减性）；
2. $F(x)$ 是一个右连续函数；
3. $\forall x \in R$，总有 $0 \le F(x) \le 1$ （有界性），且 \(\lim\limits_{x \rightarrow -\infty}F(x)=0,\lim\limits_{x \rightarrow \infty}F(x)=1\)

概率分布函数 $F(x)$ 的作用：如下图

1. 给出 $x$ 落在某区间 $(a,b]$ 内的概率：$P(a<x \le b)=F(b)-F(a)$
2. 根据 $F(x)$ 的斜率判断“区间概率” $P(A<x \le B)$ 的变化（实际上就是 概率密度函数$f(x)$）（特别注意：是判断“区间概率”，即 $x$ 落在 $(A,B]$ 中的概率，而不是 $x$ 取某个确定值的概率，这是连续型变量和离散型变量的本质区别） 某区间 $(A,B]$ 内，$F(x)$ 越倾斜，表示 $x$ 落在该区间内的概率 $P(A<x \le B)$ 越大。如图中 $(a,b]$ 区间内 $F(x)$ 的斜率最大，如果将整个取值区间以 $\delta x=b-a$ 的间隔等距分开，则 $x$ 落在 $(a,b]$ 内的概率最大。为什么？因为 $P(A<x \le B)=F(B)-F(A)$，所有区间中只有在 $(a,b]$ 这个区间上（即 $A=a，B=b$）$F(B)-F(A)$ 达到最大值，也就是图中竖向红色线段最长。

#待整理笔记