向量运算

最后修改于 2023-11-23

阅读量:[object Object]

向量求和

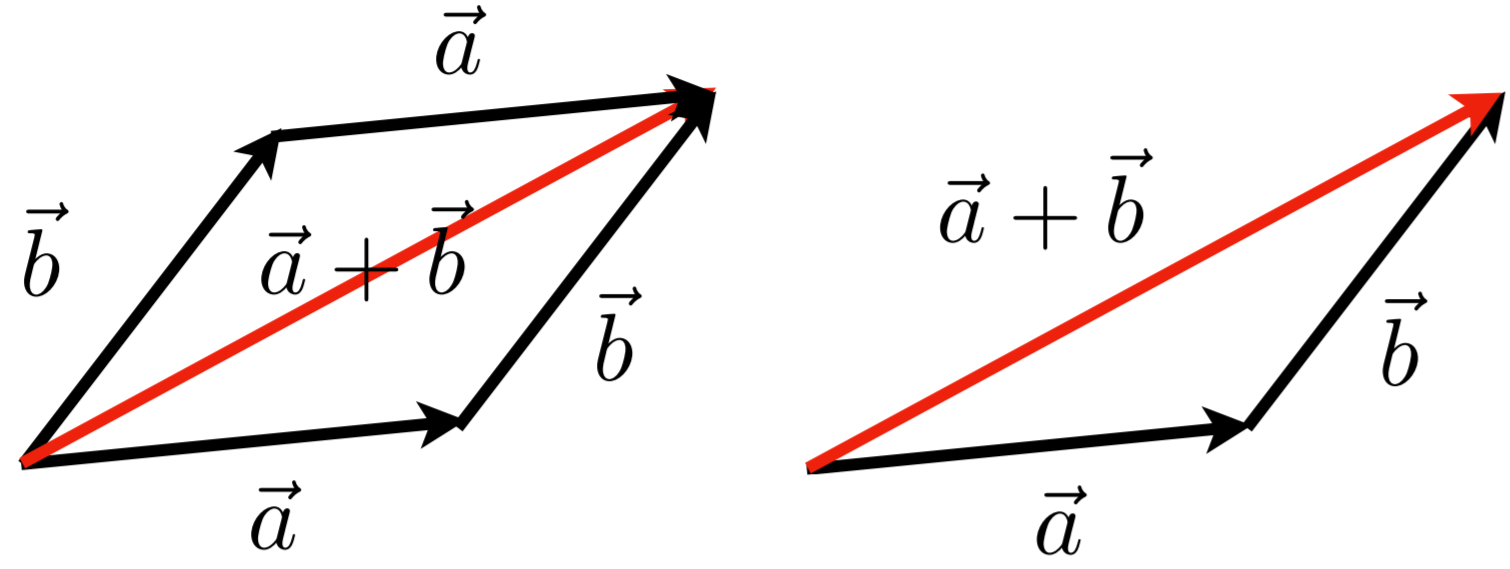
几何 Geometrically：平行四边形法则，三角形法则

代数 Algebraically：坐标相加

向量运算_figure_1.png

向量乘法

点乘 Dot (Scalar) Product

点乘结果为数量

$\vec{a} \cdot \vec{b} = ‖ \vec{a} ‖ \cdot ‖ \vec{b} ‖ c o s θ$

$c o s θ = \frac{\vec{a} \cdot \vec{b}}{‖ \vec{a} ‖ \cdot ‖ \vec{b} ‖} = \hat{a} \cdot \hat{b}$

向量点乘符合交换律、分配律和结合律。

在笛卡尔坐标系下：

$\vec{a} \cdot \vec{b} = (\begin{matrix} x_{a} y_{a} \end{matrix}) \cdot (\begin{matrix} x_{b} y_{b} \end{matrix}) = x_{a} x_{b} + y_{a} y_{b}$

$\vec{a} \cdot \vec{b} = (\begin{matrix} x_{a} y_{a} z_{a} \end{matrix}) \cdot (\begin{matrix} x_{b} y_{b} z_{b} \end{matrix}) = x_{a} x_{b} x_{c} + y_{a} y_{b} y_{c}$

作用：

找到两个向量间的夹角
找到一个向量在另一个向量上的投影

叉乘 Cross (Vector) Product

叉乘的结果是一个向量，是与两个原始向量正交的向量。

$\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}$

$‖ \vec{a} \times \vec{b} ‖ = ‖ \vec{a} ‖ ‖ \vec{b} ‖ s i n ϕ$

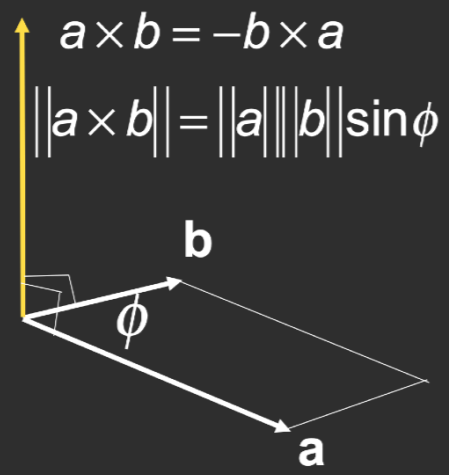
向量运算_figure_2.png

结果向量的方向由右手法则决定，四指沿被乘向量（算式中第一个向量）以小于 180 角的方向绕至叉乘向量（算式中第二个向量），此时拇指所指方向即为结果向量的方向。

向量叉乘不符合交换律，符合分配律和结合律。

向量叉乘其本身得到是与其自身正交的零向量。

在笛卡尔坐标系下：

$\vec{a} \times \vec{b} = (\begin{matrix} y_{a} z_{b} - y_{b} z_{a} z_{a} x_{b} - x_{a} z_{b} x_{a} y_{b} - y_{a} x_{b} \end{matrix})$

作用：

构建直角坐标系，通过右手法则构建的坐标系为右手坐标系，结果向量方向相反时为左手坐标系。 $\vec{x} \times \vec{y} = + \vec{z}$
判定一个向量在另一个向量的左右，乘积为正向左，为负向右（逆时针向左，顺时针向右）。
判定一个点在一个多边形的内外。按顺序依次连接点与多边形的各个顶点，判断从被连接的顶点出发的两个向量的方位，重复直至完成所有顶点的判断，均在同侧时为内，反之为外。

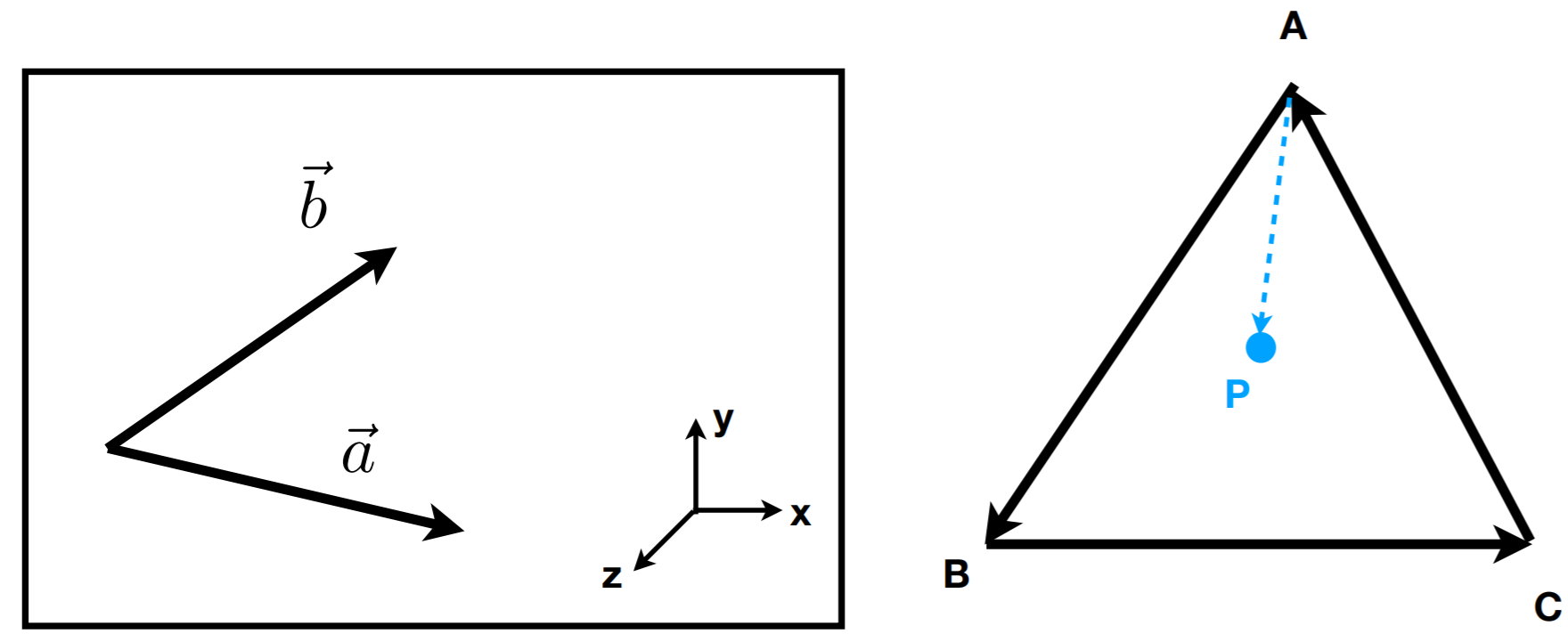
正交坐标系

可用来进行向量分解

$‖ \vec{u} ‖ = ‖ \vec{v} ‖ = ‖ \vec{w} ‖ = 1$

$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{w} = \vec{u} \cdot \vec{w} = 0$

$\vec{w} = \vec{u} \times \vec{v}$ （右手坐标系）

$\vec{p} = (\vec{p} \cdot \vec{u}) \vec{u} + (\vec{p} \cdot \vec{v}) \vec{v} + (\vec{p} \cdot \vec{w}) \vec{w}$

向量投影

$\vec{b_{⊥}}$ 是向量 $\vec{b}$ 在向量 $\vec{a}$ 上的投影，则：

$\vec{b_{⊥}}$ 的方向与向量 $\vec{a}$ 相同。
$\vec{b_{⊥}} = k \vec{a}$ ， $k = ‖ \vec{b_{⊥}} ‖ = ‖ \vec{b} ‖ c o s θ$

作用：

分解向量
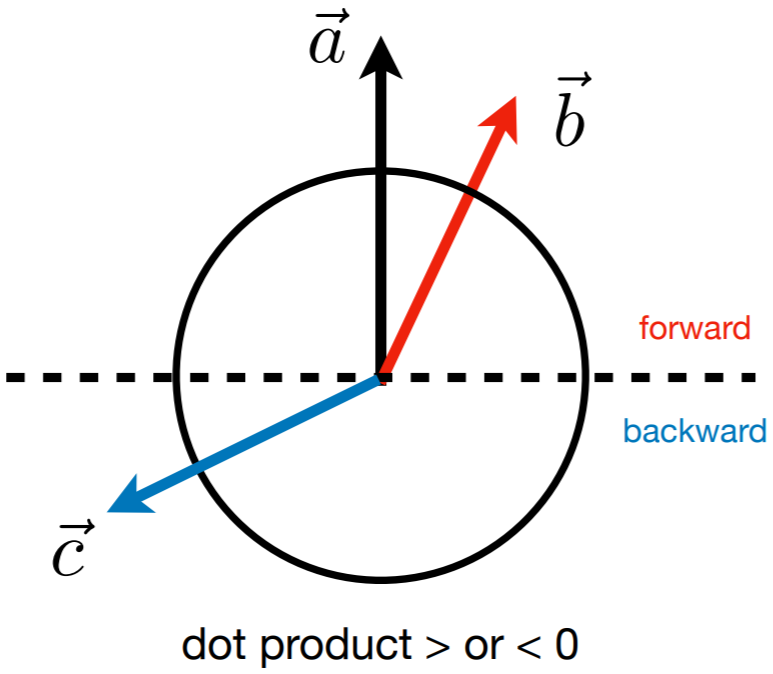
评价两个向量方向的接近程度，[-1, 1]，-1 为完全相反，0 为垂直，1 为完全相同。
决定前向和后向。

向量乘法的矩阵形式

\vec{a} \cdot \vec{b} = {\vec{a}}^{T} \cdot \vec{b} = (\begin{matrix} x_{a} & y_{a} & z_{a} \end{matrix}) (\begin{matrix} x_{b} \\ y_{b} \\ z_{b} \end{matrix}) = (x_{a} x_{b} + y_{a} y_{b} + z_{a} z_{b})

\vec{a} \times \vec{b} = A^{*} \cdot \vec{b} = (\begin{matrix} 0 & - z_{a} & y_{a} \\ z_{a} & 0 & - x_{a} \\ - y_{a} & x_{a} & 0 \end{matrix}) (\begin{matrix} x_{b} \\ y_{b} \\ z_{b} \end{matrix})

反向链接

Vector 向量

#播种

到头儿啦~